This is a followup to last week's post. I had two very good conversations with Michael Cohen and Jon Schneider that led to some more refined questions.

Conjecture 2 is false

Jon Schneider pointed out to me a construction that disproves Conjecture 2. For the alphabet \( \{ A, B \} \), consider the function \( f: [0, 1] \times \{A,B\} \to [0, 1] \) defined by \( f(x, A) = \frac{x+1}{4} \) and \( f(x, B) = \frac{x + 2}{4} \). So the string 'A' maps to \( \frac{1}{4} \), the string 'AB' maps to \( \frac{9}{16} \), and so on. Notice that every string will have a value of less than \( \frac{2}{3} \), and every nonempty string has a value of at least \(\frac{1}{4}\).

So every string of length at least 2 ending in 'A' will lie within the interval \( [\frac{5}{16}, \frac{5}{12}) \), and every string of length at least 2 ending in 'B' will lie within the interval \( [\frac{9}{16}, \frac{2}{3}) \). This means that we can find an interval around the string 'A', say \( (0, \frac{5}{16}) \) that doesn't contain the image of any other string. Similarly, we can do the same around 'B' with the interval \( (\frac{5}{12}, \frac{9}{16}) \). In fact, we'll be able to find such an open interval around every string.

What this means is that if we have an open set \( U_s \subset [0, 1] \) for every string \( s \in \{A, B\}^* \) that contains the image of \( s \) but not any other strings. So for any subset \( S \subset \{A,B\}^* \), we can define \(U = \bigcup_{s \in S} U_s\) This means that an open set can actually pick out absolutely any language, even uncomputable ones.

Is that cheating?

So of course, the next question is what additional constraint on the computation needs to be imposed so that it is a reasonable model of (for example) a recurrent neural network. One idea might be that the open set \( U \) needs to be "nice" in a sense. However, with input from Michael Cohen, I now know of some explicit constructions that decide non-regular languages.

We'll start with the language of syntactically balanced parentheses. If you're writing a program to determine whether a string is balanced, you'd keep a counter of open parentheses, and require that the count never goes negative and that it ends at zero. However, we can actually encode the count as a number in \( [0, 1] \) with continuous functions to increment and decrement.

For example, we can encode a count of \( n \) with \( \frac{1}{n+1} \). We don't need to worry about negative counts, as we can have a "deadness" parameter in our state that will always result in the string being rejected if the count ever would go negative. Since there is a gap between 1 (how we represent a count of 0) and \( \frac{1}{2} \) (how we represent a count of 1, we can continuously transition between how we handle 0 and how we handle 1, regardless of how different they are.

Here is Haskell code that implements the idea:

increment x = if x == 0 then 0 else 1/(1/x + 1)
decrement x = if x >= 1/2 then 1 else 1/(1/x - 1)

balancedParensTransition (x, d) c =
    case c of
        '(' -> (increment x, d)
        ')' -> (decrement x, min 1 (d + deadContribution x))
        _ -> (x, 1)
    where
    deadContribution x = if x >= 3/4 then 4*x - 3 else 0

balancedParensAccept (x, d) = x > 3/4 && d < 1/2

balancedParens :: String -> Bool
balancedParens = balancedParensAccept . foldl' balancedParensTransition (1, 0)

So we can use a real number as a counter, but we can actually do even better and use the bits essentially as a stack. For that we'll look at the language of balanced parentheses and brackets. In this case, we want to hold a stack of open parens and open brackets that we've seen so far.

To do this, we'll draw a tree in the compact space \( [0, 1] \times [0, 1] \).

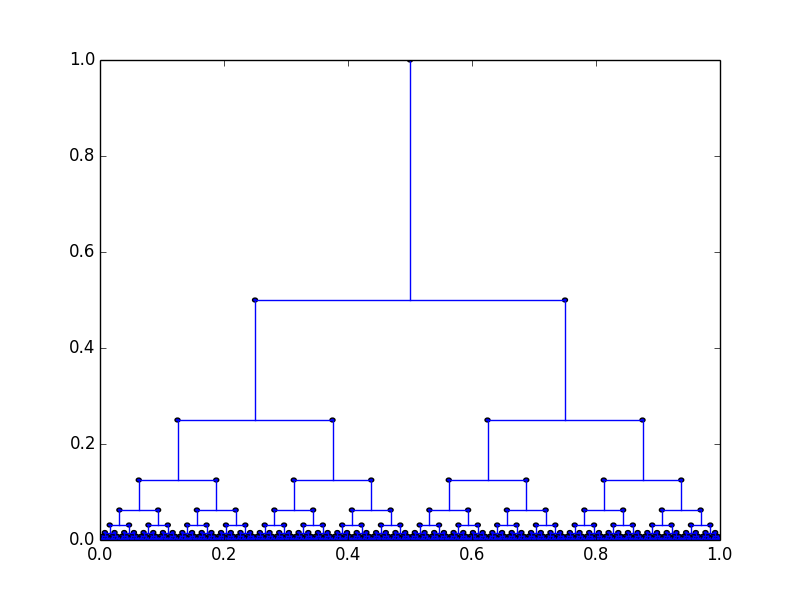
The stack is represented in the path from the top of the tree to the current position, which a left branch meaning an open paren and a right branch meaning an open bracket. It isn't too difficult to see that we can write continuous functions that move down or up the tree, but we need to be able to add deadness in a continuous fashion. This is a little bit more worrying than it sounds, because of the continuity condition at the bottom of the square. However, we can solve this by adding less and less deadness as we're farther down the tree, and doubling deadness as we move up the tree to amplify it back to the full range.

In order to pick out the last bit in the stack in a continuous fashion, we can use the y-coordinate to tell us how far down the tree we are. Here is a graph of the function \( f(x,y) = y(1 - \sin(\pi x/y)) \):

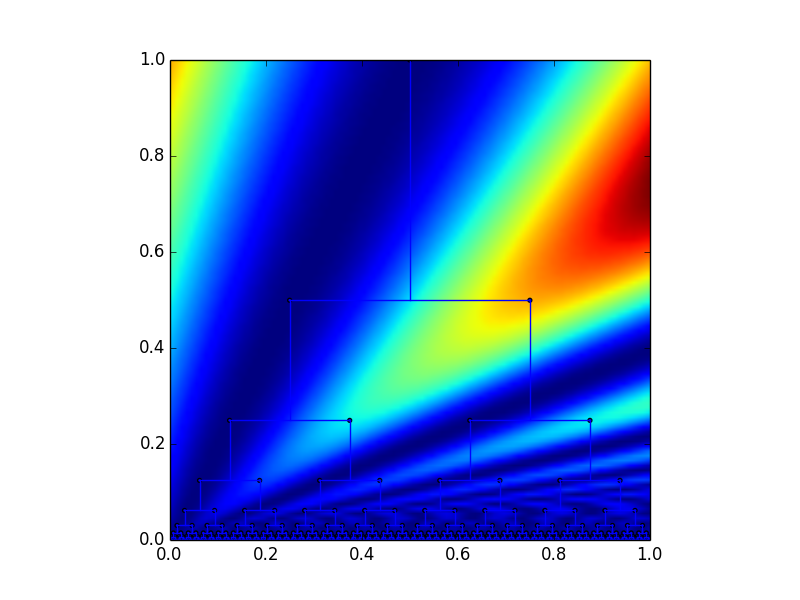
Notice how this effectively picks out all of the nodes that are right children. Similarly we can use the function \( f(x,y) = y(1 + \sin(\pi x/y)) \) to pick out left children.

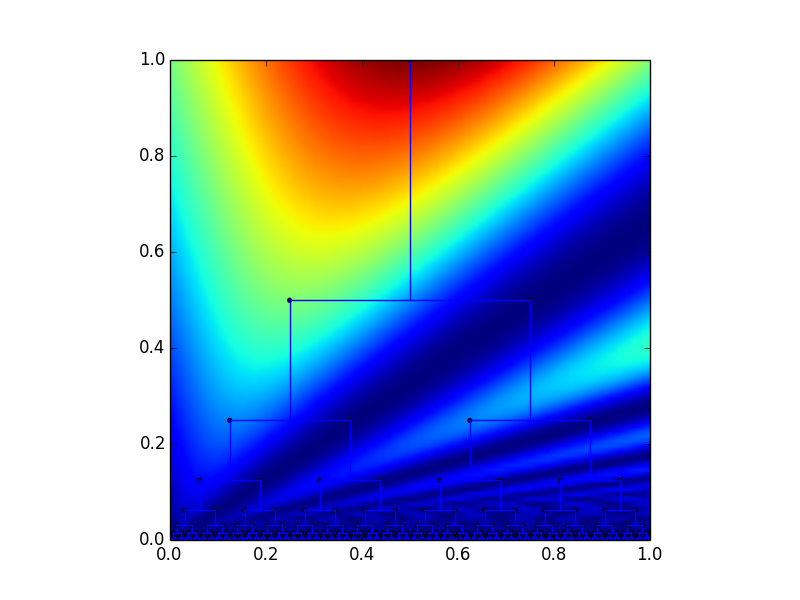
This allows us to check for a mismatch each time we encounter a close paren or a close bracket, and set the deadness parameter accordingly.

Here is Haskell code putting it all together:

balancedParensBracketsTransition (x, y, d) c =
    case c of
        '(' -> (clamp (x - y/4), y/2, d/2)
        '[' -> (clamp (x + y/4), y/2, d/2)
        ')' -> (clamp (x + y/2), clamp (2*y),
                clamp (2*d + (if y == 0 then 0 else y*(1 - sin(x*pi/y)))
                           + (if y >= 3/4 then 4*y-3 else 0)))
        ']' -> (clamp (x - y/2), clamp (2*y),
                clamp (2*d + (if y == 0 then 0 else y*(1 + sin(x*pi/y)))
                           + (if y >= 3/4 then 4*y-3 else 0)))
        _ -> (x, y, 1)
    where
    clamp = max 0 . min 1

balancedParensBracketsAccept (x, y, d) = y > 3/4 && d < 1/2

balancedParensBrackets :: String -> Bool
balancedParensBrackets =
    balancedParensBracketsAccept . foldl' balancedParensBracketsTransition (1/2, 1, 0)

So what?

This demonstrates that real (or even rational) numbers, even over a compact region and enforcing continuous transitions, can act as stacks. With two stacks, we can represent the tape of a Turing machine, meaning that with arbitrary precision numbers, even restricting \( U \) to be nice doesn't rule out arbitrary computation. This paper appears to use this idea to prove that recurrent neural nets can, in fact, simulate Turing machines.

So then the question is whether this kind of program can actually be learned by a recurrent neural network, or if there's a learning barrier. Both Michael and Jon indicated that this idea is cheating because it's not robust to noise. In fact, this paper indicates that if you add a constant amount of noise in every iteration, the final distribution is computable, meaning that it can no longer be simulating a Turing machine.

But is this the right restriction to put on the computation? Is there a reason that any learned algorithm must be robust to noise? Or can a neural net converge toward a solution where it uses intermediate states as arbitrary amounts as storage? This paper seems to have taken the idea of adding large storage to a recurrent neural net, and achieves significant improvement over recurrent neural nets, indicating that perhaps the answer is that neural nets cannot learn these techniques on their own. Is there any work done on finding a theoretical barrier there?